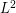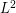In this article, we propose several quantization based stratified sampling methods to reduce the variance of a Monte-Carlo simulation. Theoretical aspects of stratification lead to a strong link between the problem of optimal  -quantization of a random variable and the variance reduction that can be achieved. We first emphasize on the consistency of quantization for designing strata in stratified sampling methods in both finite dimensional and infinite dimensional frameworks. We show that this strata design has a uniform efficiency among the class of Lipschitz continuous functionals. Then a stratified sampling algorithm based on product functional quantization is proposed for path-dependent functionals of multi-factor diffusions. The method is also available for processes made of other Gaussian processes as the Brownian bridge or an Ornstein-Uhlenbeck process. The balance between the algorithmic complexity of the simulation and the variance reduction factor has also been studied. | 
