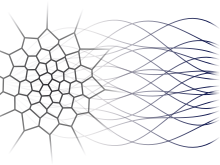
|
|
|
|
The compressed folder one_dim_1_1000.zip contains optimal quantization grids of the standard univariate normal distribution of size 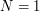 to
to 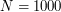 , and one_dim_1001_5999.zip from the grids of size
, and one_dim_1001_5999.zip from the grids of size 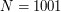 to
to 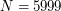 .
.
The compressed folder mult_dimensional_grids.zip contains optimized quantization grids of the standard multivariate normal distribution of size between 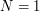 and
and 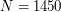 and dimension between
and dimension between 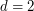 and
and 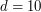 . (It does not contain the one-dimensional grids which are available separately.)
. (It does not contain the one-dimensional grids which are available separately.)
The files are in text format. In every case, the filename is N_d_nopti where N is the quantizer size and d is the dimension.
For a given size 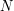 , the text files are organized as follows. It presents in the form of a matrix
, the text files are organized as follows. It presents in the form of a matrix 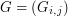 with
with 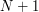 rows and
rows and 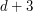 columns.
columns.
- On row
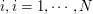 : element
: element 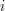 of the grid and its companion parameters.
of the grid and its companion parameters.
![$$
G_{i,1} = \left(\textrm{weight of the Voronoi cell of element } i \right)= \mathbb{P}[ \mathcal{N}(0,I_d) \in C_i(G) ].
$$](/sites/default/files/tex/a4caa9af7d4121dffd4648bc4542f576aca79150.png)
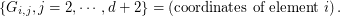


-
On last row
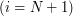 :
:
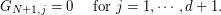

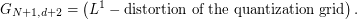
-
In particular we can verify that
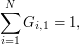
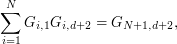
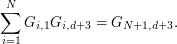
-
The multi-dimensional grids were obtained by an incremental "splitting" method based on an optimization by a mixed Lloyd-CLVQ algorithm. The splitting method consists in appending to an optimized grid of
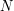 elements
elements  random points to get the starting point for the optimization procedure for a quantizer of size
random points to get the starting point for the optimization procedure for a quantizer of size 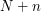 .
.
Note that the CLVQ procedure is only used for small values of
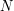 .
. -
The one-dimensional grids where obtained by deterministic methods. This is to directly minimize the quadratic distortion seen as a function of
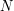 values.
Several methods are available as a tridiagonal Newton-Raphson method or a semi-closed Lloyd's algorithm. See article [1] for more details on these algorithms.
values.
Several methods are available as a tridiagonal Newton-Raphson method or a semi-closed Lloyd's algorithm. See article [1] for more details on these algorithms.